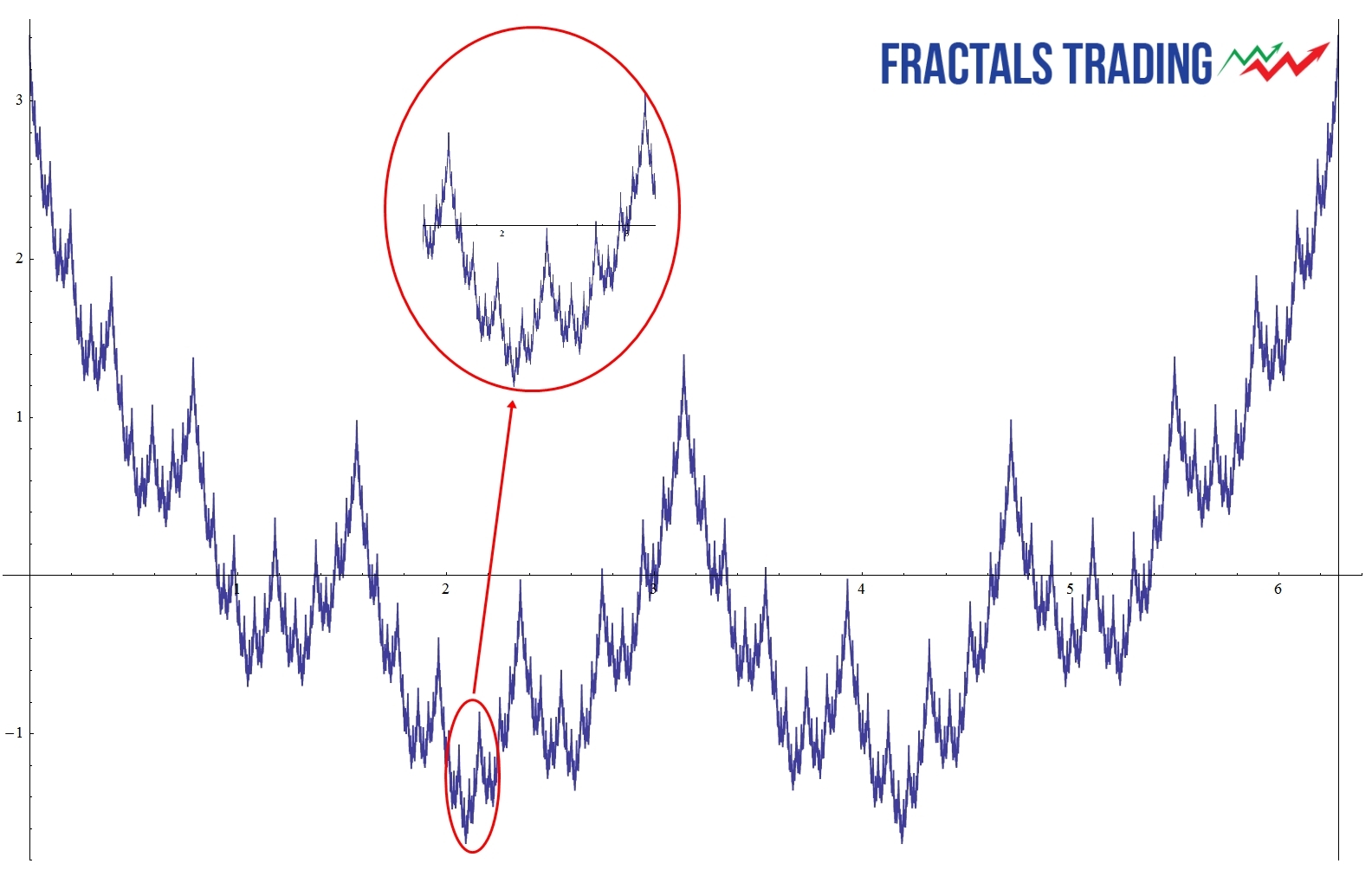
Fractal-Wave process is the representation of the Fractal geometry in the time dimension. Fractal geometry is made from a repeating pattern at many different scales. Simply speaking it is repeating patterns with varying size. Fractal geometry can be a self-similar pattern with the strictly same patterns across at every scale. Or if the pattern loosely matches to the past one, this can be still considered as fractal geometry. We call this as near self-similarity against the strict self-similarity. Many examples of Fractal geometry can be found in nature. Snowflakes, coastlines, Trees are the typical example of the Fractals geometry in space. Fractal-Wave is the fractal geometry generated in time dimension. Just like Fractal Geometry can be described by self-similar patterns. Fractal-Wave can be described by self-similar patterns repeating in time. The concept of Fractal-Wave can be illustrated well by Weierstrass function.
Loosely speaking, Weierstrass function is the cyclic function generated from infinite number of Cosine functions with different amplitude and wavelength. By combining infinite number of Cosine functions, it can generate a complex structure repeating self-similar patterns in different scales. This is a typical synthetic example of Fractal-Wave patterns with strict self-similar patterns. We present this function to help you to understand the properties of the self-similar process. The real world financial market shows the loose fractal geometry. They do not repeat in the identical patterns in shape and in size. The repeating patterns are similar to each other up to certain degree. Since Weierstrss function is the synthetic example for the strict fractal geometry, reader should note that Weierstrss function does not represent the real world financial market.